문제
매운 것을 좋아하는 Leo
모든 음식의 스코빌 지수를 K이상으로 만들고 싶음.
모든 음식의 스코빌 지수를 K이상으로 만들기 위해 Leo는 스코빌 지수가 가장 낮은 두 개의 음식을 아래와 같이 특별한 방법으로 섞어 새로운 음식을 만든다.
섞은 음식의 스코빌 지수 = 가장 맵지 않은 음식의 스코빌 지수 +( 두번째로 맵지 않은 음식의 스코빌 지수 x 2 )
모든 음식의 스코빌지수가 K 이상이 될 때 까지 반복해 섞는다
Leo가 가진 음식의 스코빌 지수를 담은 배열 scoville과 원하는 스코빌 지수 K가 주어질 때, 모든 음식의 스코빌 지수를 K 이상으로 만들기 위해 섞어야 하는 최소 횟수를 return
제한
scoville의 길이는 1~1,000,000
K는 0~1,000,000,000
scoville원소는 각각 0~1,000,000
모든 음식의 스코빌 지수 K이상으로 만들 수 없는 경우 -1 return
예시
scoville = [1, 2, 3, 9, 10, 12], K=7
1번 3, 5, 9, 10, 12
2번 9, 10, 12, 13 → 끝 : 제일 작은 요소가 7보다 크면 끝났다고 판단할 수 있다.
return 2
복잡도
최악의 경우 : 수가 하나 남을 때 까지 섞어야 하는 경우 (n-1회)
각 단계( 섞을 때 마다) 에서 요구되는 계산량 : 정렬된 리스트에 순서 맞춰 원소를 삽입( )
전체 풀이의 복잡도 : → 높다!
최소/최대 원소를 빠르게 꺼내는 방법 → Heap구조를 사용
•
Heap : 최대/최소 원소를 빠르게 찾을 수 있음
◦
max heap : 최대 원소 빠르게 꺼낼 수 있음
◦
min heap : 최소 원소 빠르게 꺼낼 수 있음
◦
연산
▪
힙 구성(heapify)
▪
삽입(insert)
▪
삭제(remove)
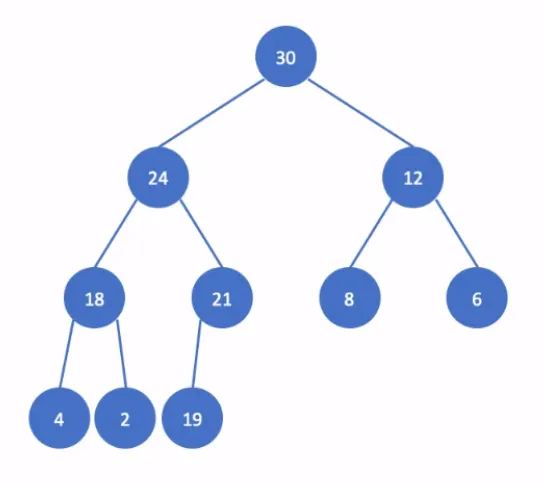
[heap의 구현 예] ( max heap )
자세한 내용은 자료구조 참고
그림을 보면, 완전 이진트리(complete binary tree)로, 배열을 이용해 구현이 가능하다.
[heap 응용]
정렬(heapsort)
우선 순위 큐(priority queue) : 들어가는 순서와 달리 나오는 순서는 우선순위에 따름
Python에서 heap 사용하기
import heapq
heapq.heapify(L) # list L로부터 min heap 구성
m = heapq.heappop(L) # min heap L에서 최소값 삭제+반환
heapq.heappush(L, x) # min heap L에 원소 x 삽입
Python
복사
풀이
import heapq
def solution(scoville, K):
answer = 0
heapq.heapify(scoville)
while True:
'''
반복문 중단 조건
1. 모든 스코빌지수가 K이상
2. 스코빌지수 하나 남았는데 K 이상이 안됌.
'''
min1 = heapq.heappop(scoville)
if min1 >= K:
break
elif len(scoville) == 0:
answer = -1
break
min2 = heapq.heappop(scoville)
new_scoville = min1 + 2*min2
heapq.heappush(scoville, new_scoville)
answer += 1
return answer
Python
복사
[이 코드의 복잡도]
최악의 경우 while문이 n번 반복되고
heappop, heappush는 이므로
전체는
heap이 아닌 list를 사용해 배열하고, 최소값 꺼낸 후, 새로 만들어진 지수를 순서에 맞춰 끼워넣는 식으로 구현하면, 가 될 것