동적계획법이란?
•
문제의 답인지 확인하기 위해 확인해야하는 범위(solution space)를 진전하며 동적으로 설정하는 것
•
주어진 최적화 문제를 재귀적인 방식으로 보다 작은 부분문제로 나누어 부분 문제를 풀어 이 해를 조합하여 전체 문제의 해답에 이르는 방식
•
알고리즘의 진행에 따라 탐색해야 할 범위를 동적으로 결정함으로써 탐색 범위를 한정할 수 있다.
•
수학과 컴퓨터 과학, 그리고 경제학에서 동적 계획법이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다. 위키백과
ex) 피보나치 수열
사실 좋은 예는 아니지만 간단한 예
재귀함수로 구현한다면?
f(4) = f(3) + f(2)
= f(2) + f(1) + f(1) + f(0)
= f(1) + f(0) + f(1) + f(1) + f(0)
복잡도가 지수형태로 나타남. 비효율적
동적계획법을 적용한다면?
f(0) = 0, f(1) = 1
f(2) = f(1) + f(0) = 1
f(3) = f(2) + f(1) = 2
f(4) = f(3) + f(2) = 3
복잡도 : 선형함수 형태
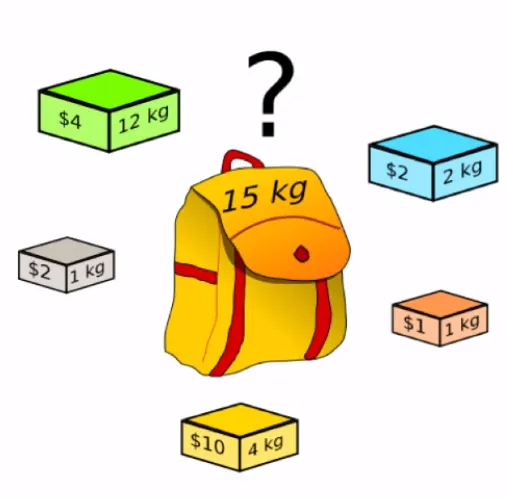
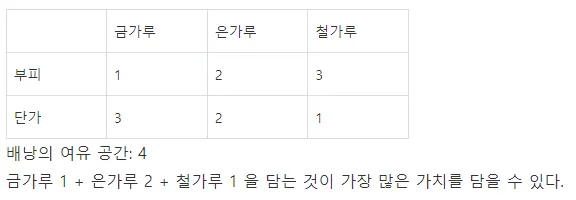
ex) Knapsack Problem
배낭 문제는 조합 최적화의 유명한 문제이다. 간단하게 말하면, 한 여행가가 가지고 가는 배낭에 담을 수 있는 무게의 최댓값이 정해져 있고, 일정 가치와 무게가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다. 위키백과
1.
쪼갤 수 있는 경우 → 탐욕법(greedy algorithm)
부피 대비 가치가 높은 물건 순서대로 담으면 된다. 뒤에 어떤 물건을 넣을지 고려하지 않아도 되기 때문
현재 가장 이익이 되는 행동만 되면 되기 떄문에
2.
쪼갤수 없는 경우 → 동적계획법
def knapsack(capacity, size, value, n):
if capacity == 0 or n == 0:
return 0
if size[n-1] > capacity:
return knapsack(capacity, n-1)
else:
return max(value[n-1] + knapsack(capacity-size[n-1], n-1),knapsack(capacity, n-1)
size = [3, 4, 7, 8, 9]
value = [4, 5, 10, 11, 13]
knapsack(10, size, value, 5) # 14
Python
복사
•
하나를 배낭에 넣었을 때 가치의 증가량 + 다음 항목 검색 함수
•
배낭에 넣지 않고 다음을 검색하는 함수
•
둘 중 큰 값을 선택해 return
문제
5와 사칙연산만으로 12 표현하기
12 = 5 + 5+ (5/5) + (5/5)
12 = 55/5 + 5/5
12 = (55+5)/5
5를 사용한 횟수는 각각 6, 5, 4회
가장 작은 경우 4회
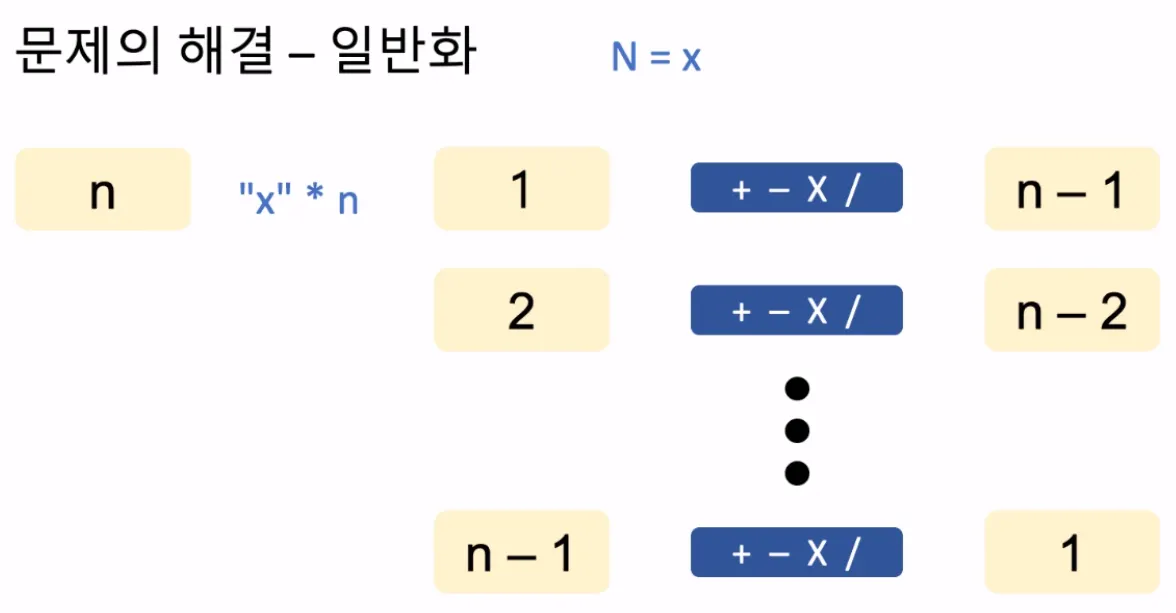
숫자 N과 number가 주어질 때 N과 사칙연산만 사용해 표현할 수 있는 방법 중 N 사용횟수의 최솟값을 return
제한
N은 1~9
number는 1~32000
수식엔 괄호화 사칙연산만 가능하고 나누기 연산에선 나머지는 무시
최솟값이 8보다 크면 -1 return
[예시]
N=5, number=12, return 4 → 문제의 예시
N=2, number=11, return 3 → 11 = 22 / 2
풀이
동적계획법
N을 한 번 사용해서 만들 수 있는 수 (들) : 1
N을 두 번 사용해서 만들 수 있는 수 (들) : 2
N을 세 번 사용해서 만들 수 있는 수 (들) : 3
... 반복
ex) N=5
1번 : 5
2번 : 55(붙이기), 10(더하기), 0(빼기), 25(곱하기), 1(나누기)
3번 : 555(붙이기) 1번사용해만든수 + - x / 2번사용해만든수
2번사용해만든수 + - x / 1번사용해만든수
⇒ 60, 15, 5, 30, 6, -5, -20, 4, 275, 50, 0, 125, 11, 2, 20, -4, 555
(중복값없도록 set로 구현)
4번 : 5555(붙이기), 1번사용해만든수 + - x / 3번사용해만든수
2번사용해만든수 + - x / 2번사용해만든수
3번사용해만든수 + - x / 1번사용해만든수
4번 : 5555(붙이기), 1번사용해만든수 + - x / 4번사용해만든수
2번사용해만든수 + - x / 3번사용해만든수
3번사용해만든수 + - x / 2번사용해만든수
4번사용해만든수 + - x / 1번사용해만든수
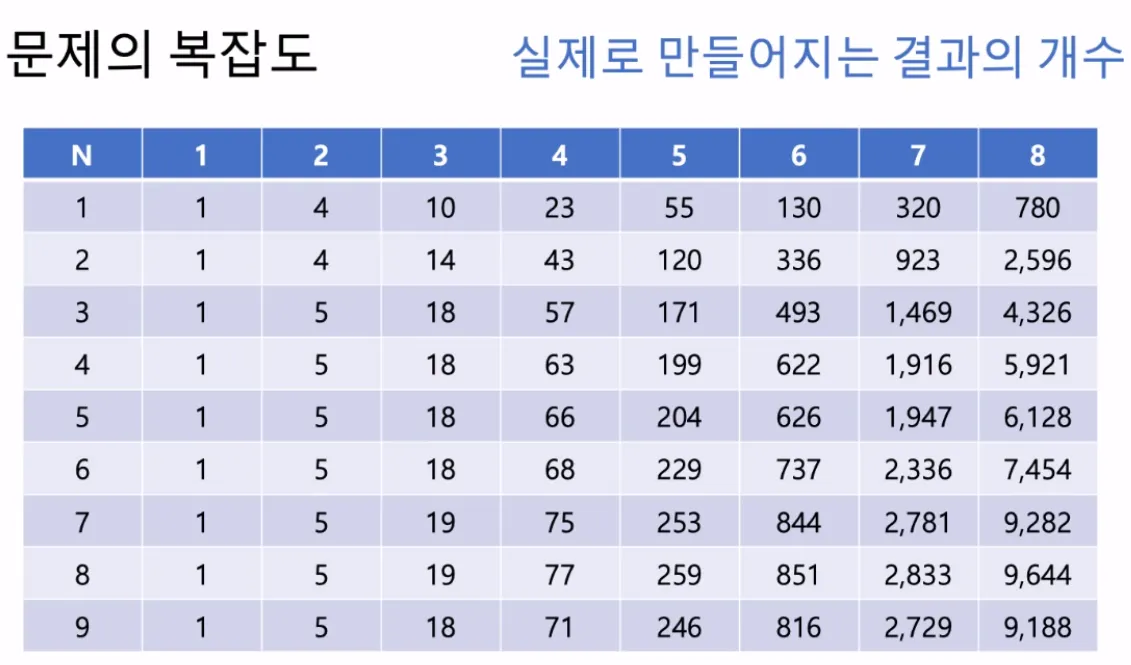
이렇게 하면 조합을 모두 나열하기 때문에, 괄호가 있는 경우, 없는 경우, 모두 고려하게 된다
문제의 성질에 따라, 동적계획법으로 풀어냄으로써 탐색해야 하는 범위를 효과적으로 줄일 수 있다.
풀이
code
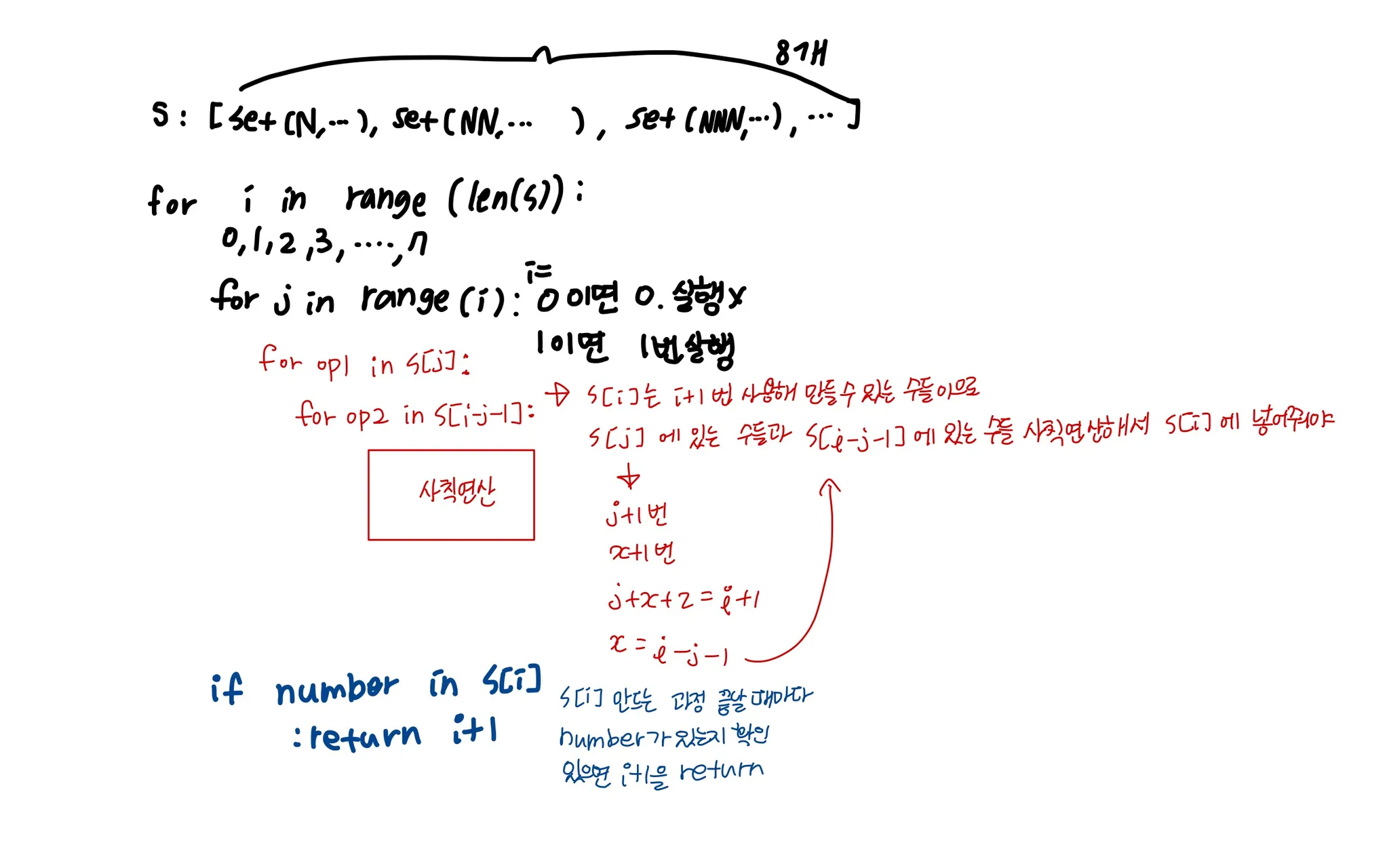
def solution(N, number):
s = [set() for x in range(8)] # set 8개 들어있는 list
# s[i]는 N을 i-1번 사용해 만들 수 있는 수들의 집합
for i, x in enumerate(s, start=1):
# 각 set에 N을 i번 반복한 수를 넣어줌
# 각 set은 일단 각각 N, NN, NNN, NNNN, ... 의 수를 가지고 시작
x.add(int(str(N)*i))
for i in range(len(s)):
for j in range(i):
for op1 in s[j]:
for op2 in s[i-j-1]:
s[i].add(op1 + op2)
s[i].add(op1 - op2)
s[i].add(op1 * op2)
# op2가 0이면 나눌 수가 없으니까
if op2 != 0:
s[i].add(op1 // op2) # 나머지는 버리기
if number in s[i]:
return i+1
# 반복문이 끝났다는 건 s[i]들에 number가 없었던 것이므로
return -1
Python
복사